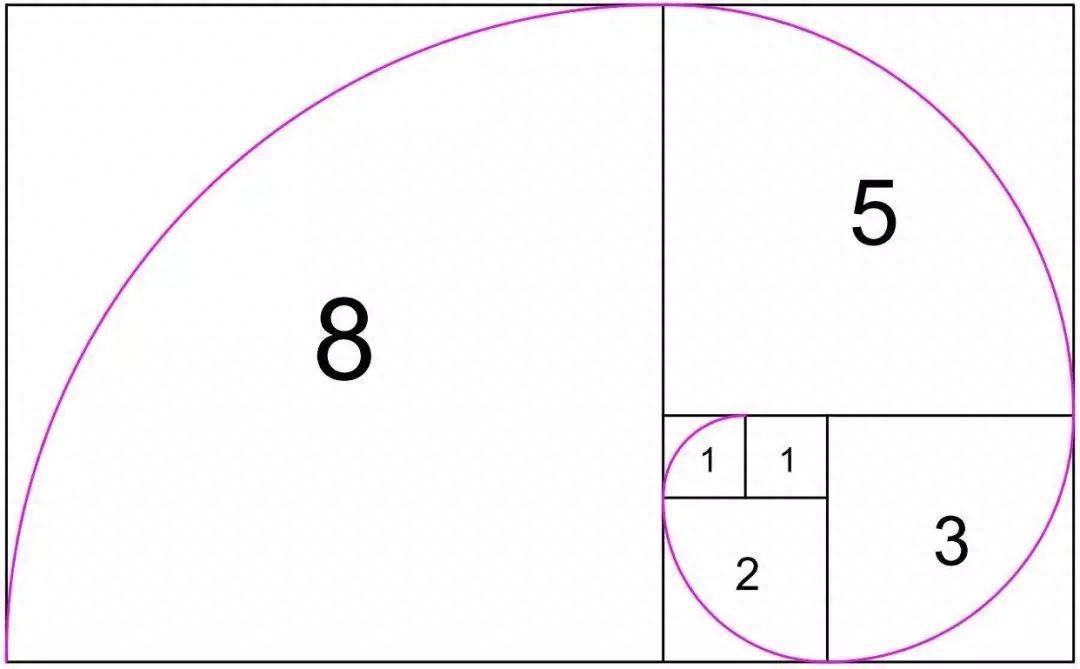
斐波那契列数列
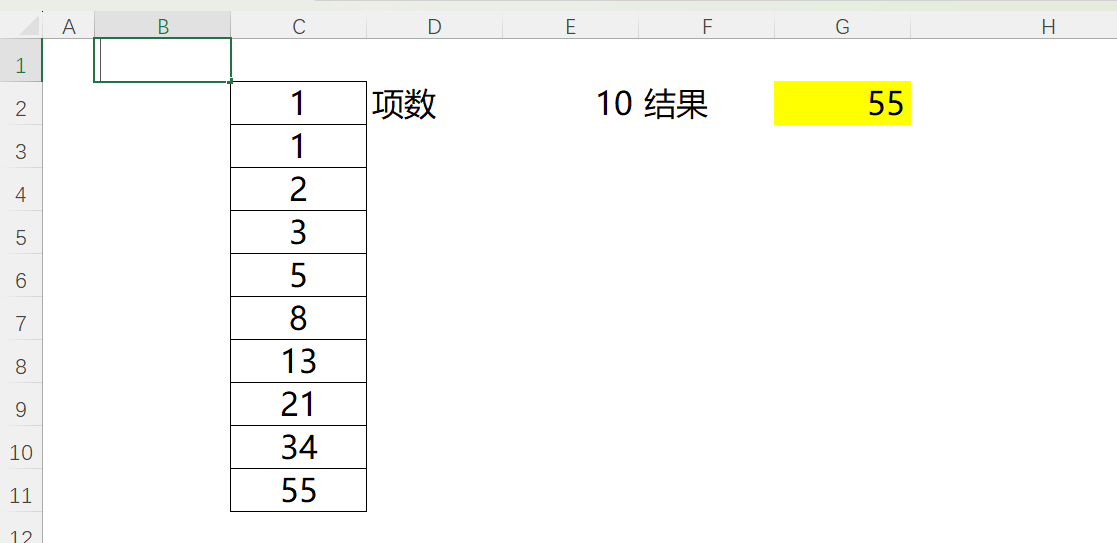
如表格中,斐波那契数列(英文:Fibonacci sequence),又称黄金分割数列,因出自于意大利数学家斐波那契的一道兔子繁殖问题而得名。斐波那契数列指的是形如的数列。这个数列的前两项为1,从第3项开始,每一项都等于前两项之和:1、1、2、3、5、8、13、21、34……如何求得每一项的结果,公式如下:
=LET(FX,LAMBDA(digui,x,IF(x<3,1,digui(digui,x-1) digui(digui,x-2))),
FX(FX,E2))
公式思路:
本例主要讲的是lambda递归的用法。递归就是指调用自身直到条件不符合为止的算法。lambda函数对递归的支持使函数具备了一门编程语言的所有算法:条件、循环、递归。
本例中的FX变量就是一个递归变量,它在过程中调用FX本身来参与计算,直到符合x<3这个条件,才会将数值相加,得出结果。
现在的office365最大的改进之处是支持了使用let函数直接调用递归函数,而不是像以前一样需要将递归函数放在名称管理器里,这样函数的编写就更加直接,更加容易编辑出来,以为递归函数的广泛使用提供了条件。这就是说在excel中实现递归有两种方法,一是直接写出来,另一种办法是使用名称管理器:
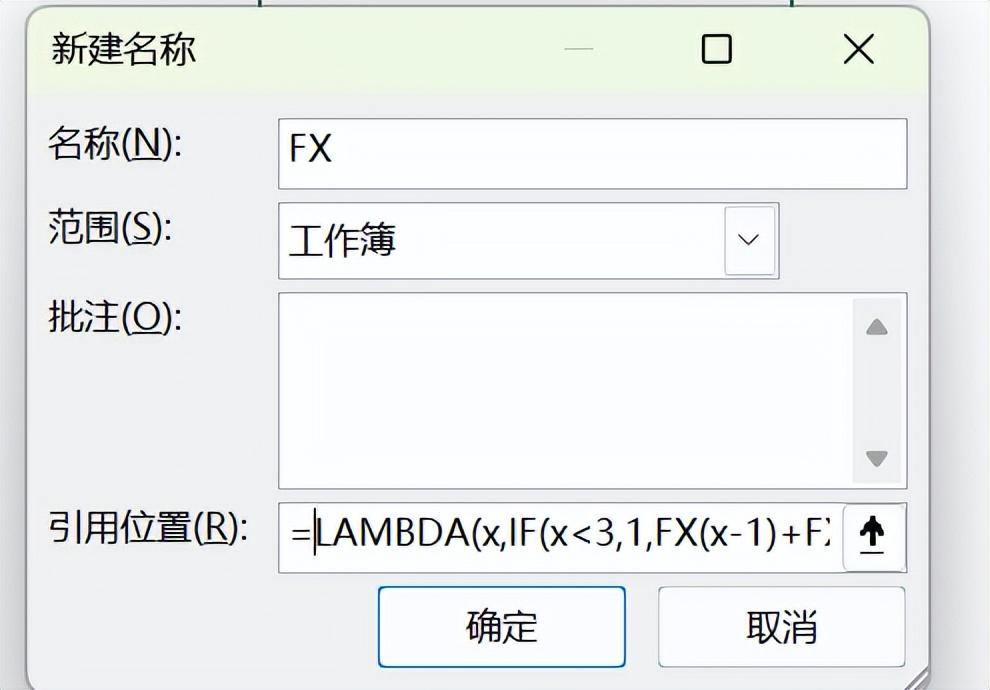
在引用位置输入:=LAMBDA(x,IF(x<3,1,FX(x-1) FX(x-2)并在结果单元格中输入FX(E2),也可以得到结果。
对比两种方法我们可以看出直接输入法比较快捷,但对digui这个形式参数的理解有很高的要求,这并不传递表格中实现的数值,只是调用递归的形参,由于它的存在,递归函数本身的调用也会发生一些变化 。
第二种方法需要调用对话框,需要交互式填入,可能效率低一些,可调试性差一些,但更加的直观。
你喜欢哪一种呢,欢迎评论区中交流。










评论 (0)