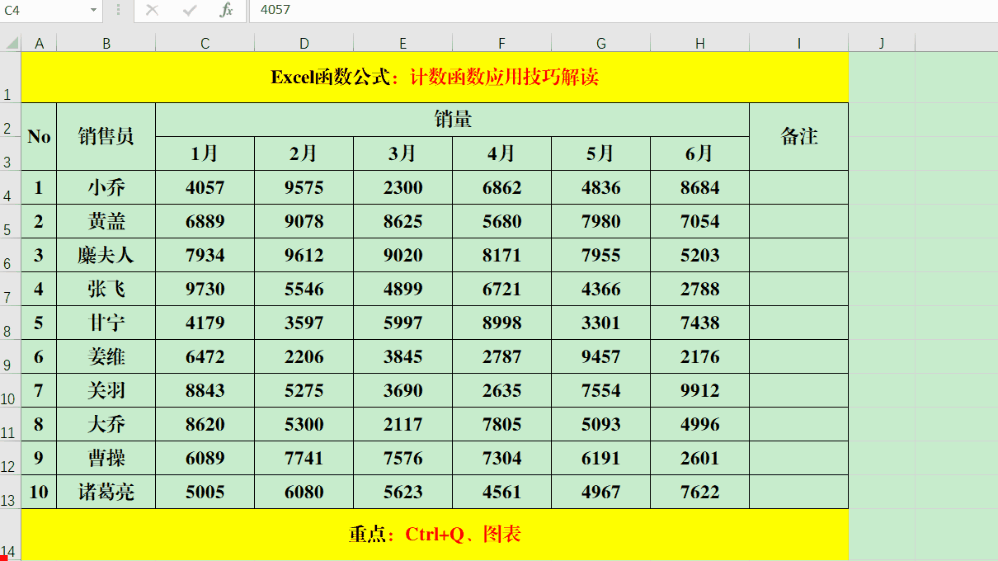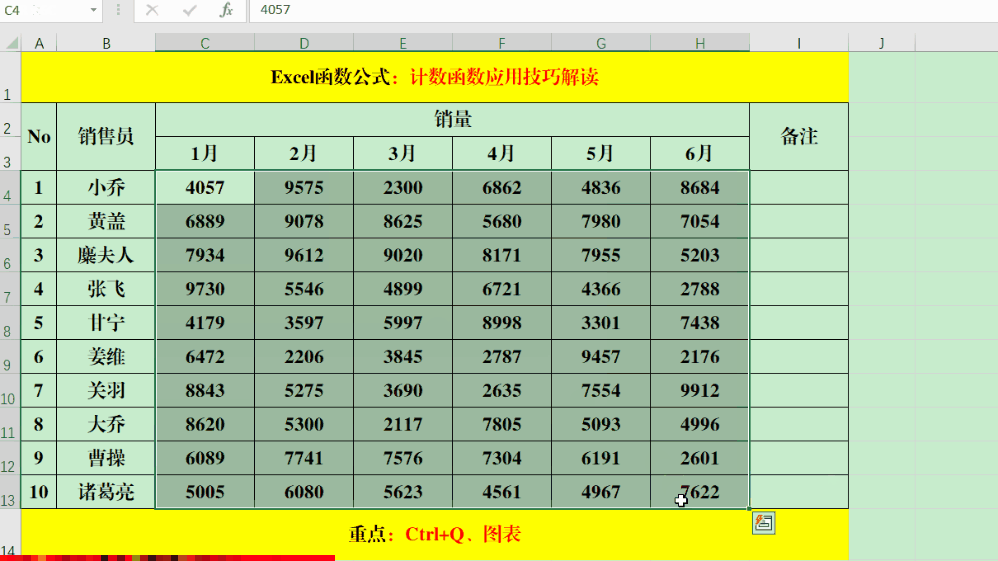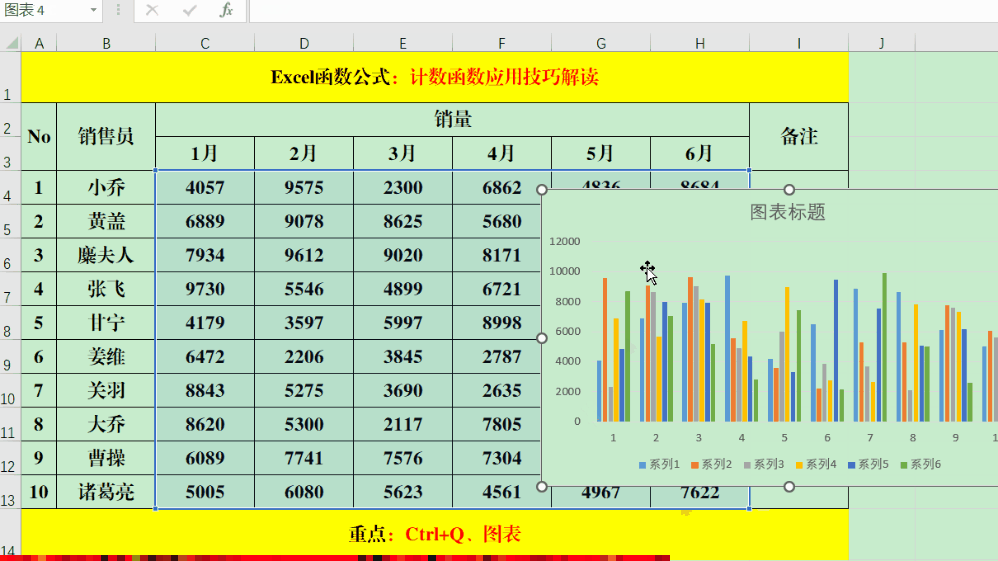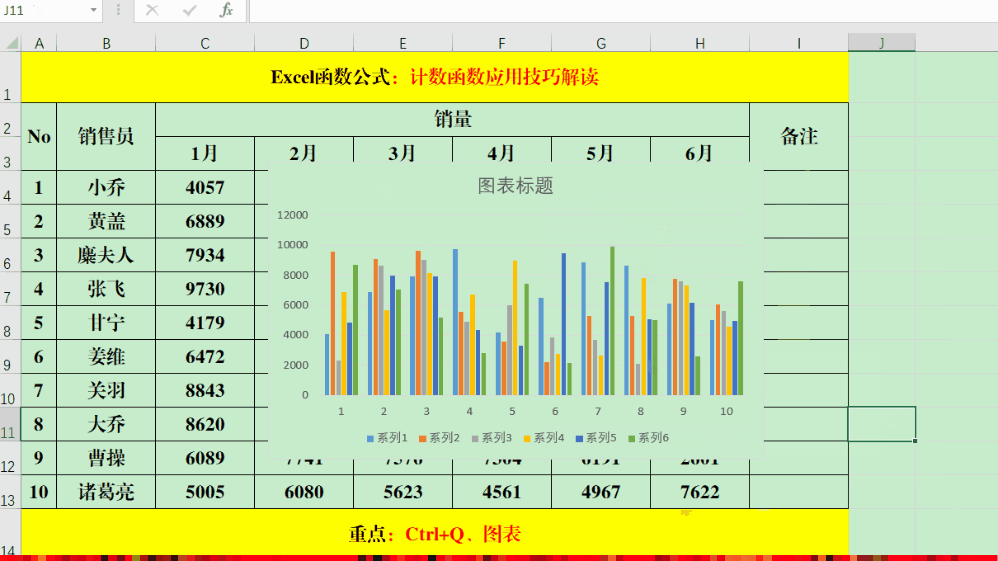
在 Excel 丰富的函数体系中,数学和三角函数板块犹如一座宝藏库,而 EXP 函数则是其中专注于自然指数运算的一颗璀璨明珠。无论是在科学研究、金融分析,还是工程计算等领域,涉及到以自然常数e为底数的指数运算场景,EXP 函数都能发挥关键作用,为数据处理和分析提供强大支持。
一、函数功能
EXP 函数的核心使命是返回自然常数的次幂。这里的常数约等于 2.71828182845904,是自然对数的底数。在许多数学和科学问题中,以e为底的指数函数有着广泛的应用,比如在描述生物种群增长、放射性衰变等自然现象的数学模型中,EXP 函数就成为了不可或缺的计算工具。
二、语法结构
EXP 函数的语法简洁明了,呈现为:EXP (number) 。这种简洁的语法形式,使得用户在使用时能够轻松上手,只需将需要作为指数的数值作为参数输入即可。
三、参数说明
参数 Number:这是 EXP 函数唯一的参数,它代表应用于底数e的指数。该参数可以是各种实数类型,包括整数、小数、逻辑值(在计算时会自动转换为数值)等,丰富的数据类型支持使得 EXP 函数在不同的运算场景中都能灵活应用。
四、注解要点
其他底数幂的计算:如果我们需要计算以其他常数为底的幂,Excel 提供了更为便捷的指数操作符 “^”。例如,若要计算常数3的2次幂,只需在相应单元格中输入 “=3^2”,即可快速得到结果。这种多样化的计算方式,满足了用户在不同场景下对幂运算的需求。
与 LN 函数的关系:EXP 函数与计算自然对数的 LN 函数互为反函数。这意味着,如果先对一个数使用 LN 函数得到(即y=LN(x)),再对y使用 EXP 函数,将得到原始的数x(即EXP)(y)=x)。这种紧密的数学关系,在一些复杂的数学运算和数据处理中,为我们提供了灵活转换和验证结果的方法。
五、示例详解
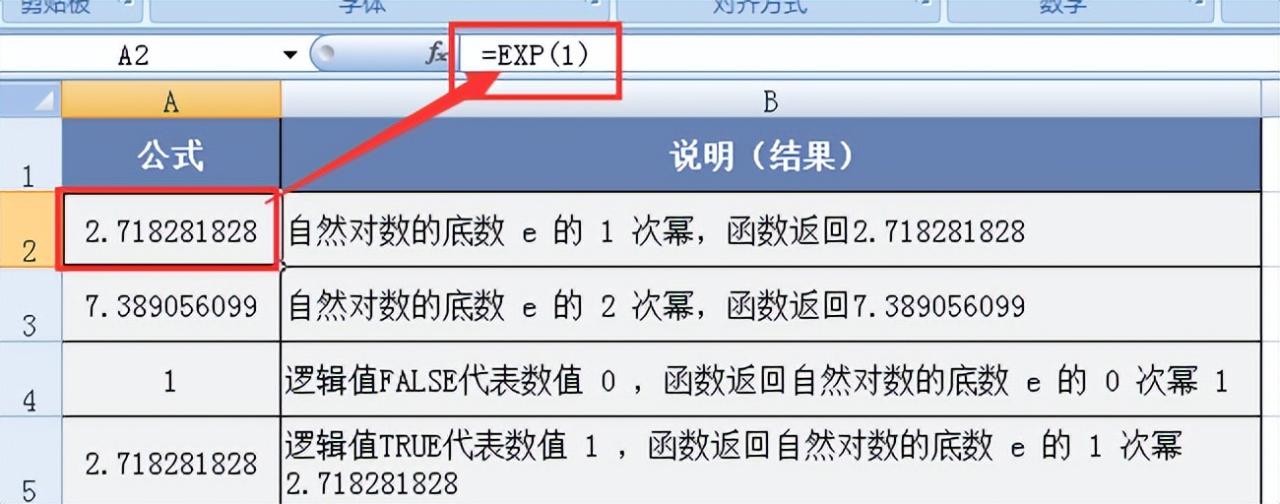
图例 1:求自然对数的底数e的次幂。在 Excel 中输入 “=EXP (1) ”,函数迅速返回2.718281828,这与自然常数的值基本一致,验证了函数在计算e的一次幂时的准确性。
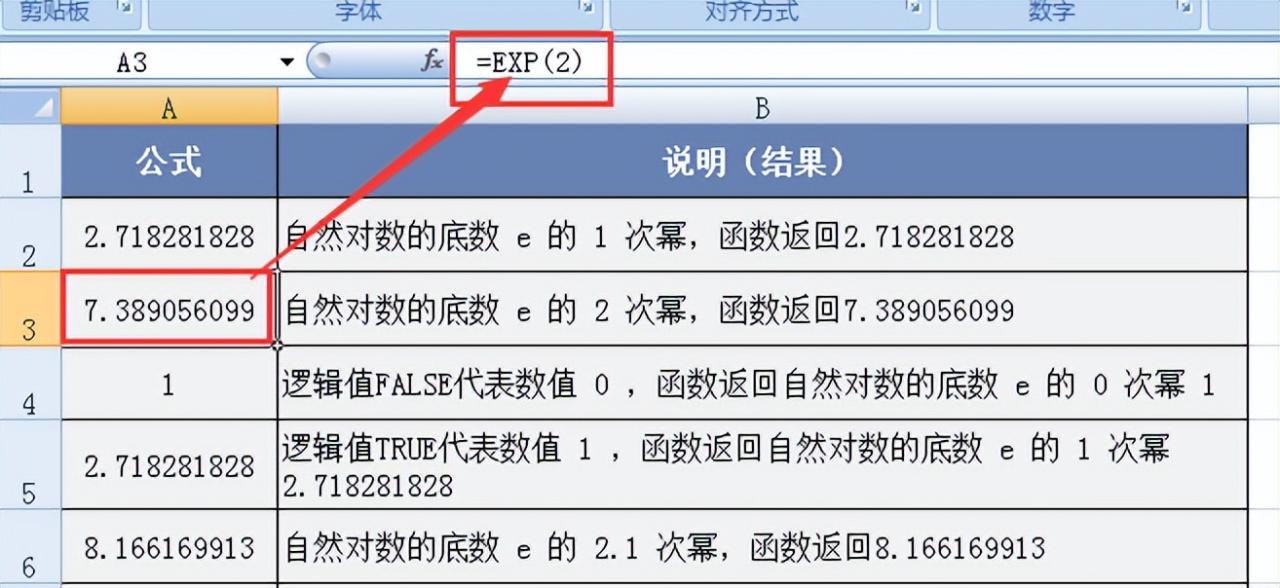
图例 2:求自然对数的底数e的2次幂。输入 “=EXP (2) ”,函数返回7.389056099,展示了函数对整数指数的有效计算能力,清晰地呈现了e的二次幂的数值结果。
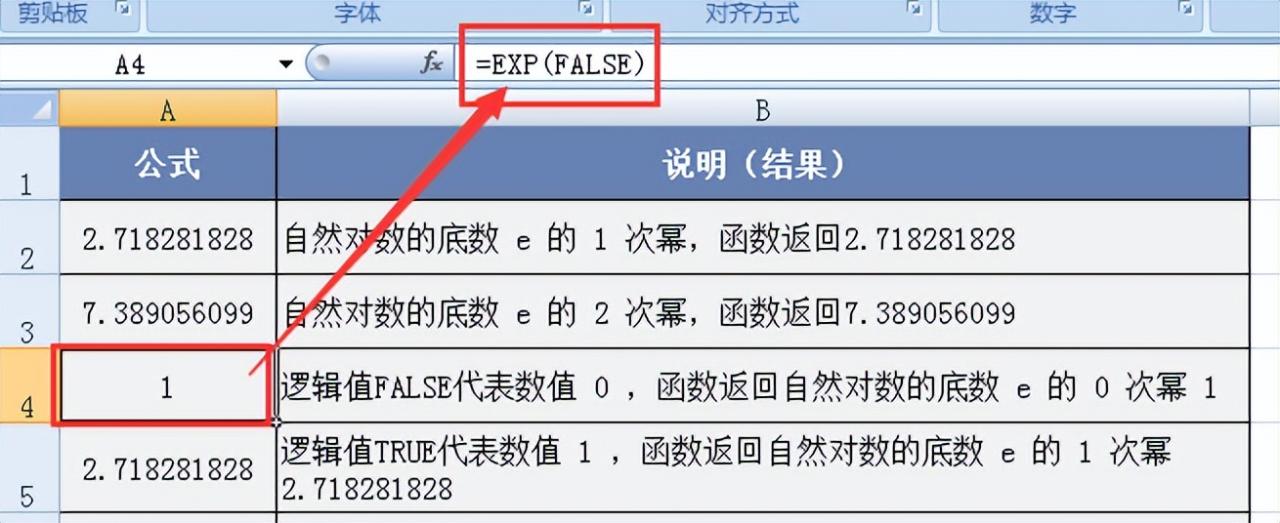
图例 3:由于逻辑值 FALSE 在 Excel 中代表数值0,当使用 “=EXP (FALSE) ” 时,函数返回自然对数的底数e的0次幂1。这体现了函数对逻辑值的自动转换和正确计算,展示了其在处理不同数据类型时的灵活性。
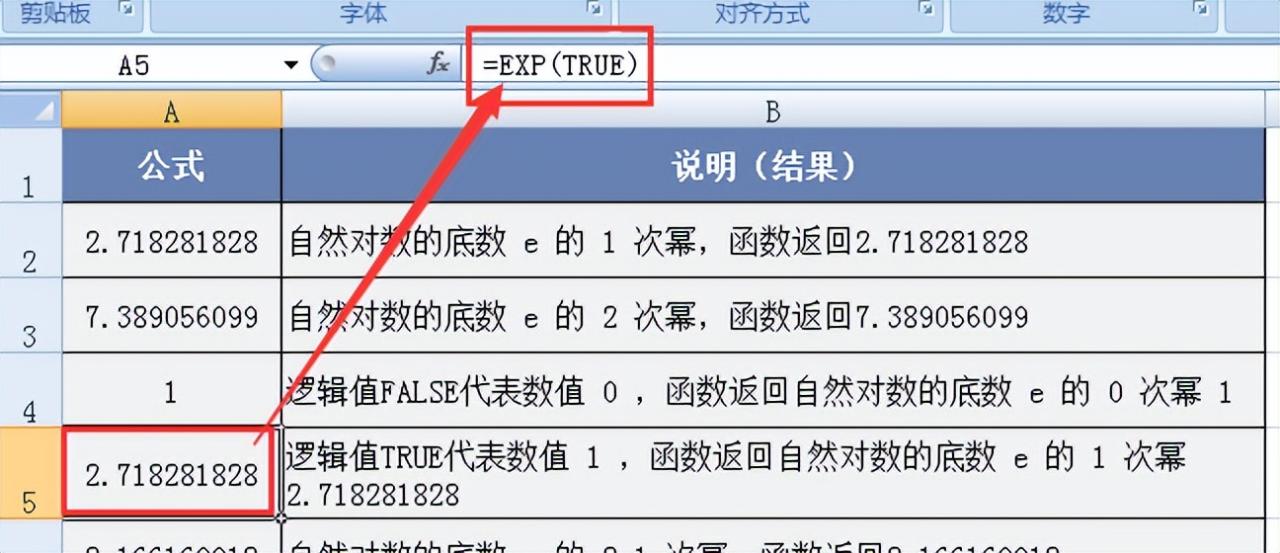
图例 4:逻辑值 TRUE 在 Excel 中代表数值1,输入 “=EXP (TRUE) ”,函数返回自然对数的底数e的1次幂 2.718281828,再次验证了函数对逻辑值转换为数值后进行指数运算的准确性。
图例 5:求自然对数的底数e的2.1次幂。通过输入 “=EXP (2.1) ”,函数返回8.166169913,展示了函数对小数指数的精确计算能力,满足了在实际应用中对非整数指数运算的需求。
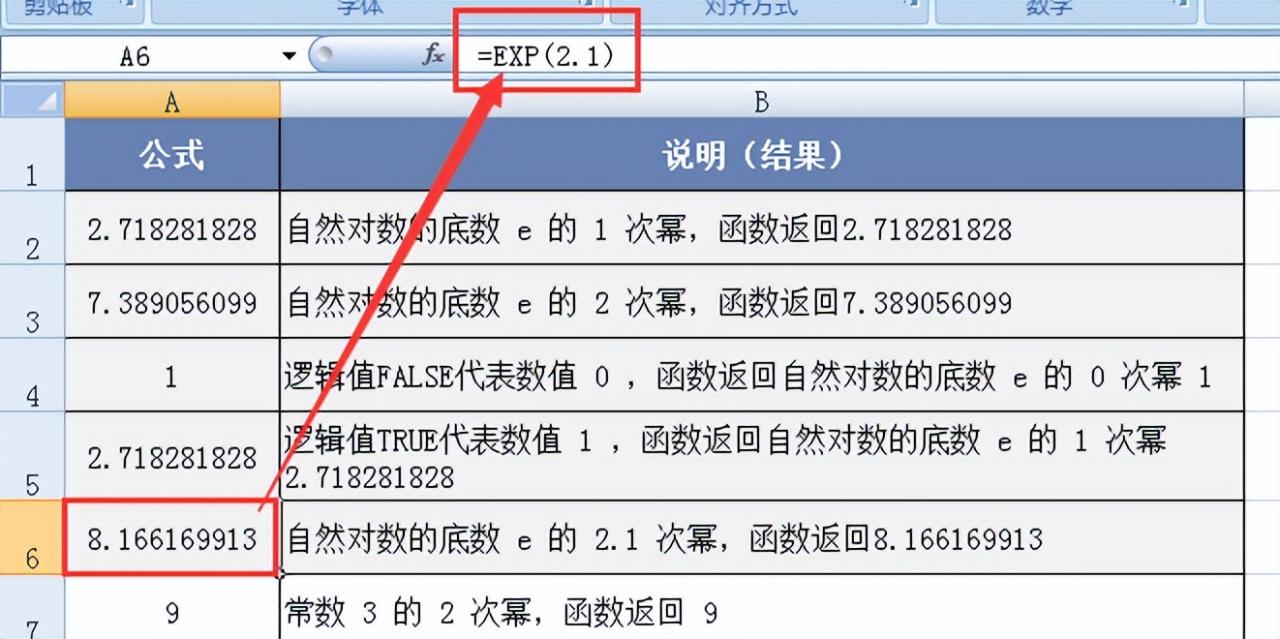
图例6:其他自然常数的幂计算表达式
求自然数3的2次幂
图例 6:
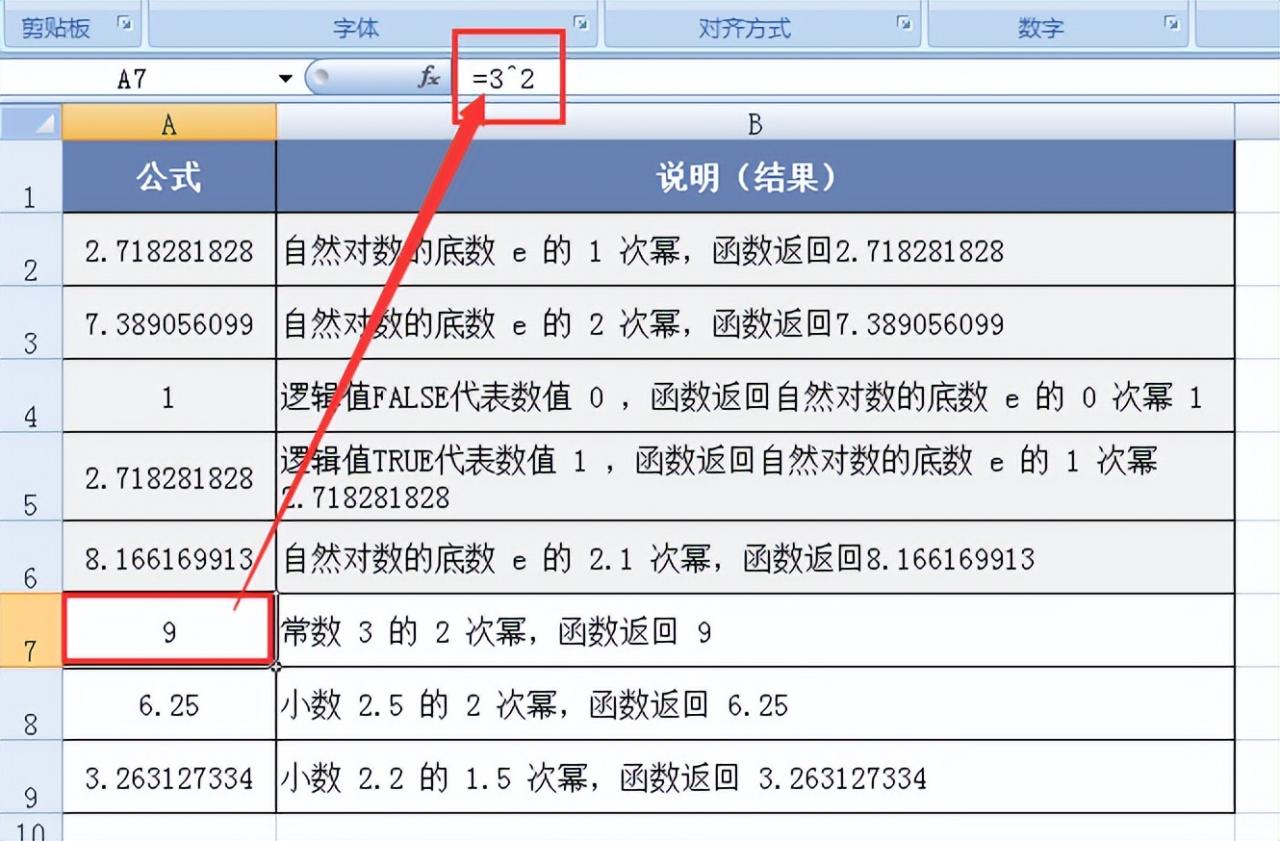
求自然数3的2次幂:使用指数操作符 “^”,在单元格中输入 “ =3^2 ”,得到结果9,直观地展示了以其他常数为底的幂的计算方法。
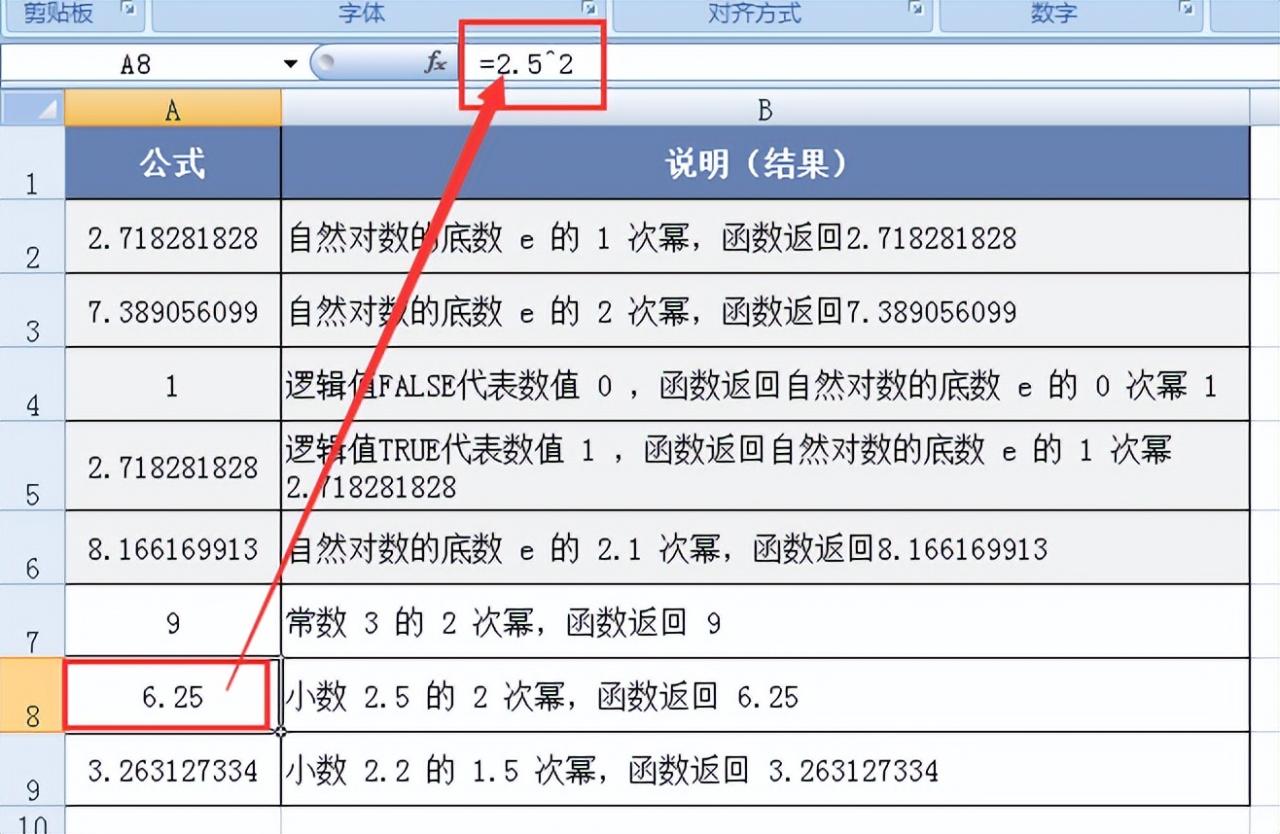
求小数2.5的2次幂:输入 “=2.5^2”,返回结果6.25,体现了指数操作符对小数底数和整数指数的运算能力。
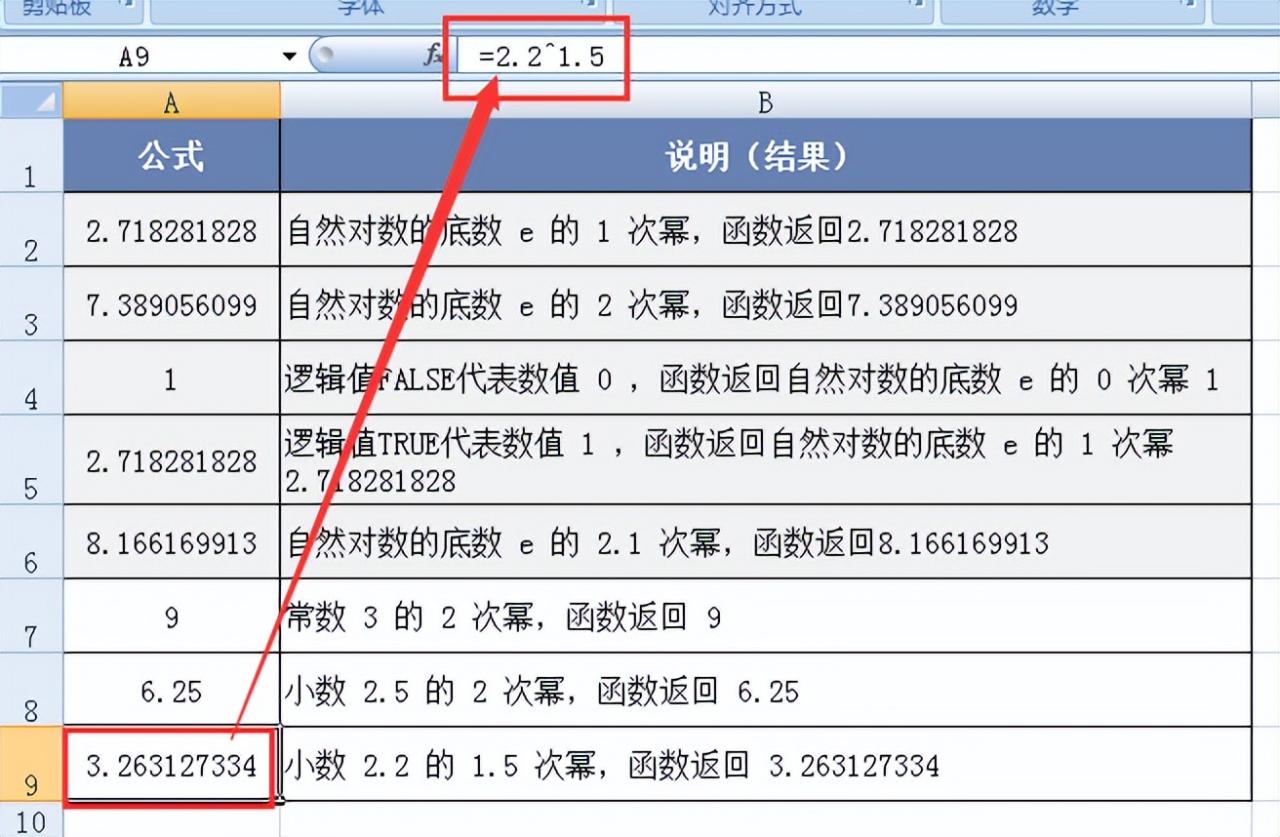
求小数2.2的1.5次幂:输入 “=2.2^1.5”,得到结果约为3.234830465,进一步展示了指数操作符在处理小数底数和小数指数时的灵活性和准确性,为复杂的幂运算提供了有效手段。
通过对 EXP 函数的功能、语法、参数、注解以及丰富示例的全面探秘,我们能够深入理解并熟练运用这一函数,为解决各类涉及自然指数运算的问题提供有力支持,在数据处理、数学计算以及专业领域的分析工作中更加游刃有余。




评论 (0)