在 Excel 的函数宇宙中,数学和三角函数板块宛如一座蕴藏着无限宝藏的矿山,而 ASIN 函数便是其中一颗闪耀的明珠,专门用于解决反正弦值的计算问题。从工程设计到科学研究,再到数据分析中涉及几何角度与三角函数关系的复杂场景,ASIN 函数都发挥着不可或缺的作用。
一、函数功能
ASIN 函数肩负着返回参数反正弦值的重要使命。简单来讲,若已知一个角度的正弦值,借助 ASIN 函数便能精准求出该角度的大小。值得注意的是,这里返回的角度值以弧度为单位呈现,其取值范围被严格限定在 -π/2 到 π/2 之间。这就好比在一个直角三角形中,当我们知晓对边与斜边的比值(即正弦值)时,利用 ASIN 函数,就能迅速得出该角的弧度值,为后续深入分析三角形的特性提供关键数据。
二、语法结构
ASIN 函数的语法极为简洁,呈现为:ASIN (number) 。这种简洁明了的语法结构,极大地降低了函数的使用门槛,即便是 Excel 新手,也能在短时间内快速掌握其调用方法,在实际的数据处理工作中轻松实现高效计算。
三、参数说明
参数 Number:这是 ASIN 函数唯一的输入参数,它代表的是角度的正弦值。但需要特别留意的是,该参数的取值范围被严格约束在 -1 到 1 之间。这是基于三角函数的基本定义,正弦函数的值域本身就限定在 -1 到 1 这个区间内,超出此范围的数值根本不存在对应的反正弦值。例如,我们输入 0.6、 -0.8 等在规定区间内的数值,函数能够正常工作;而一旦输入 1.2、 -1.5 等超出范围的数值,函数将无法给出正确的计算结果。
四、注解要点
弧度与角度的转换:当我们运用 ASIN 函数获得的计算结果是以弧度形式呈现时,在某些实际应用场景中,可能更倾向于使用角度来进行衡量。此时,便有两种便捷的方法可供选择,将弧度值转换为角度值。第一种方法是将函数返回的弧度结果乘以 180/PI () ,这里的 PI () 函数专门用于返回圆周率 π 的精确数值;第二种方法则更为简便,直接调用 DEGREES 函数,它能迅速将弧度值精准转换为角度值。这两种转换方式,为我们在不同的单位需求场景下,灵活自如地处理反正弦值提供了强有力的支持。
五、示例详解
图例 1:以弧度表示 -0.5 的反正弦值。在数学知识体系中,我们清楚地知道 -0.5 的反正弦值对应的弧度是 -π/6 。在 Excel 工作表中,只需在相应单元格输入 “=ASIN (-0.5)” ,按下回车键后,函数便会迅速返回结果约为 -0.523598776 ,这与理论上的 -π/6 弧度值高度契合,有力地验证了函数在计算弧度形式反正弦值时的准确性与可靠性。
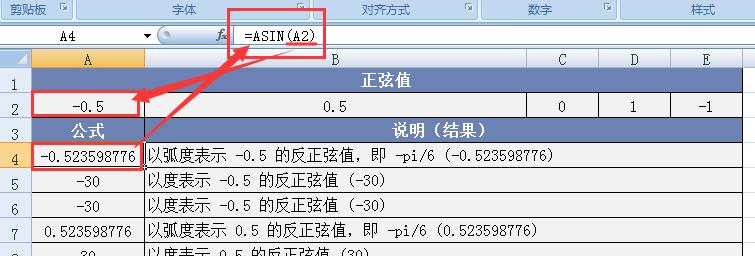
图例 2:以度表示 -0.5 的反正弦值。首先,我们通过 ASIN 函数得到 -0.5 的反正弦值的弧度形式,接着,将该弧度值乘以 180/PI ( ) 。在 Excel 中进行此操作后,我们能够得到以角度表示的结果为 -30° ,这正是 -0.5 的反正弦值在角度制下的准确数值。
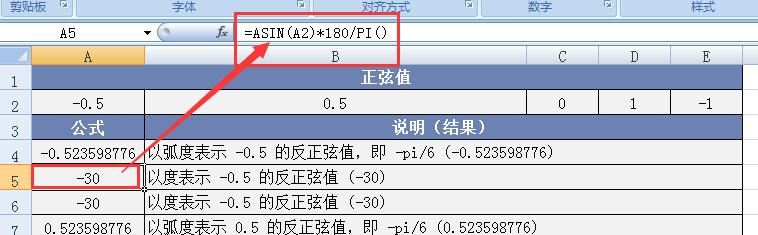
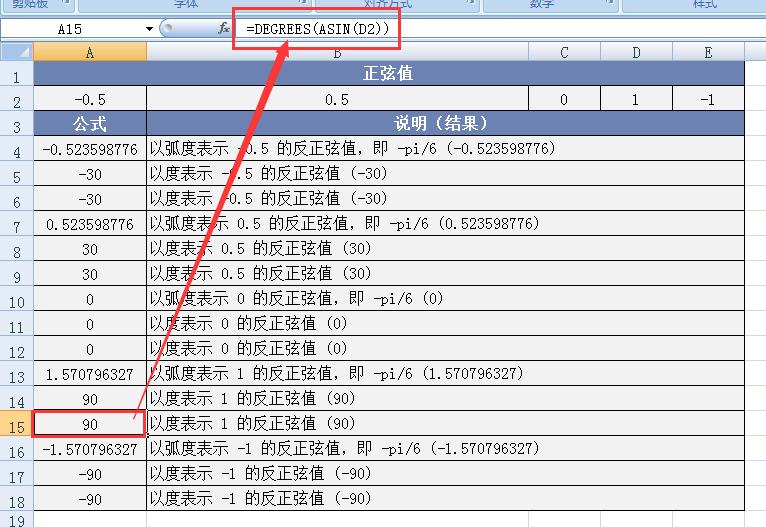
图例 3:以度表示 -0.5 的反正弦值,借助 DEGREES 函数实现。在 Excel 中,我们直接使用 “=DEGREES (ASIN (-0.5))” ,函数会自动先计算出 ASIN (-0.5) 的弧度值,然后再通过 DEGREES 函数将其精准转换为角度值,最终同样返回 -30° ,这一过程充分展示了 DEGREES 函数在弧度与角度转换过程中的便捷性与高效性。
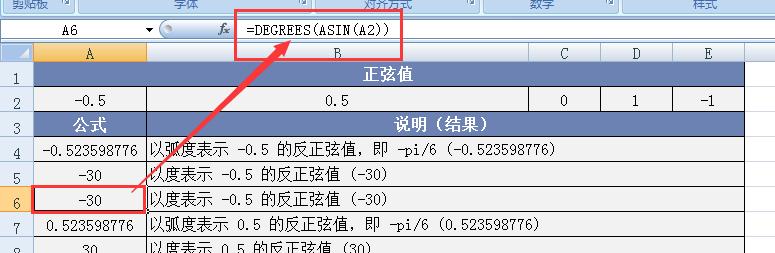
图例 4:以弧度表示 1 的反正弦值。在数学领域,我们明白 1 的反正弦值对应的弧度是 π/2 。在 Excel 中输入 “=ASIN (1)” ,函数会迅速返回结果约为 1.570796327 ,这与理论上的 π/2 弧度值高度一致,再次证明了 ASIN 函数在处理特殊值时的准确性。
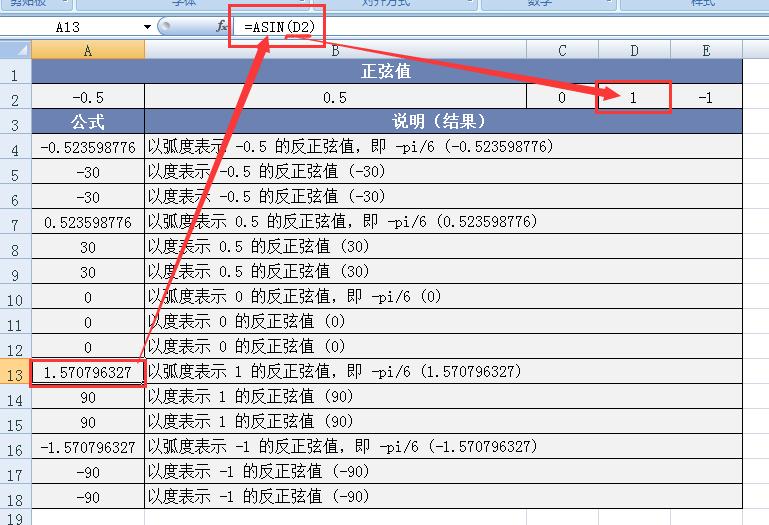
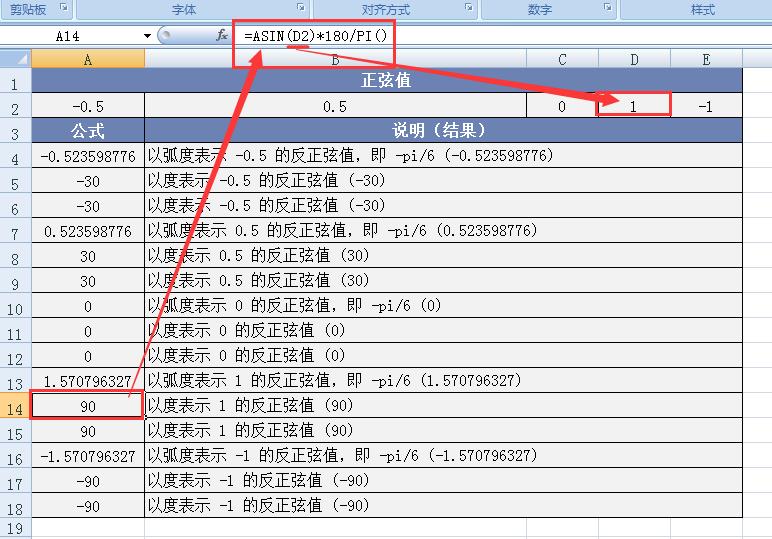
图例 5:以度表示 1 的反正弦值。我们先通过 ASIN 函数得到 1 的反正弦值的弧度形式,然后将其乘以 180/PI ( ) 。在 Excel 中完成这一系列操作后,得到的角度值为 90° ,这便是 1 的反正弦值在角度制下的正确结果。
图例 6:以度表示 1 的反正弦值,借助 DEGREES 函数实现。在 Excel 中,输入 “=DEGREES (ASIN (1))” ,函数会先计算出 ASIN (1) 的弧度值,再通过 DEGREES 函数将其转换为角度值,最终返回 90° ,这一过程清晰地展现了 DEGREES 函数在简化角度转换操作方面的显著优势。
通过对 ASIN 函数的功能、语法、参数、注解以及丰富示例的全方位、深层次剖析,我们能够透彻掌握这一函数在 Excel 中的应用技巧。这不仅能为我们解决各类涉及反正弦值计算的复杂问题提供坚实的技术支撑,还能让我们在数学计算、数据分析以及各类专业领域的工作中,更加游刃有余、高效精准地完成任务。





评论 (0)