Excel中CORREL函数用法：返回两组数据的相关系数

CORREL函数返回两个单元格区域的相关系数

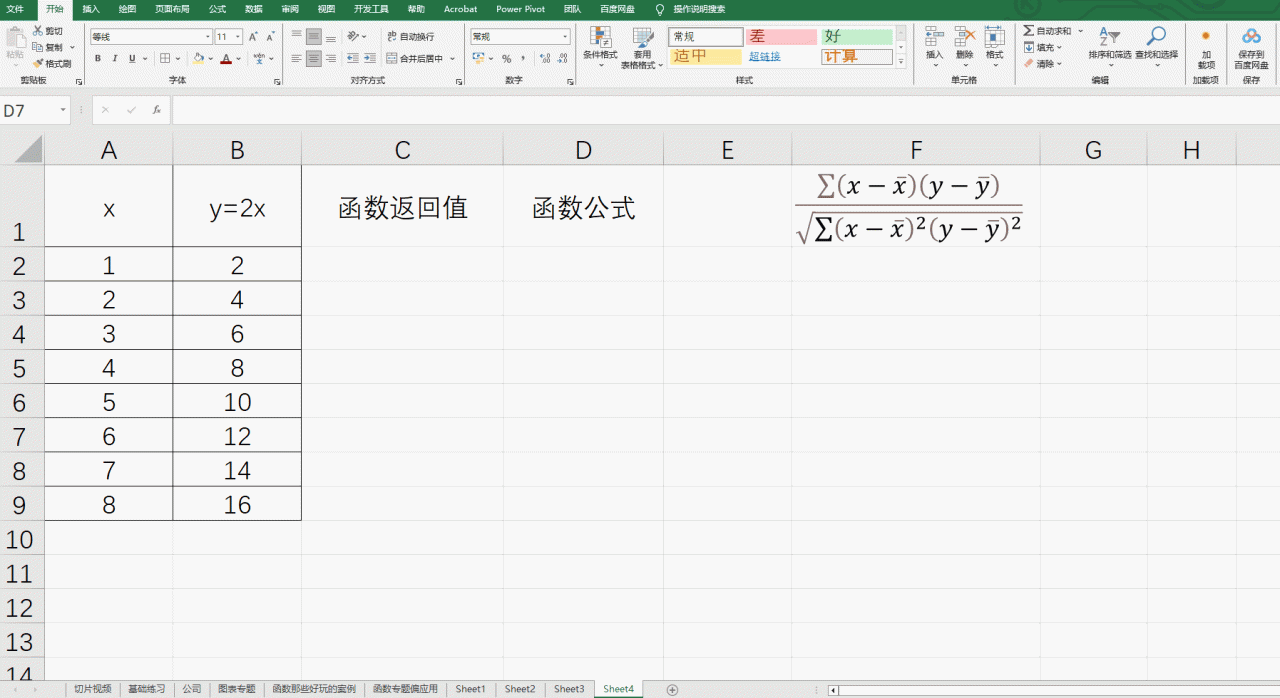
相关系数的公式为

一般相关系数大于0，我们就称正相关，相关系数小于0，就称负相关，如果是1的话，就是线性相关。

就是一条直线的变量，自变量的两组数据的相关系数是1

比如y=2x的数据，我们先通过函数返回一下相关系数

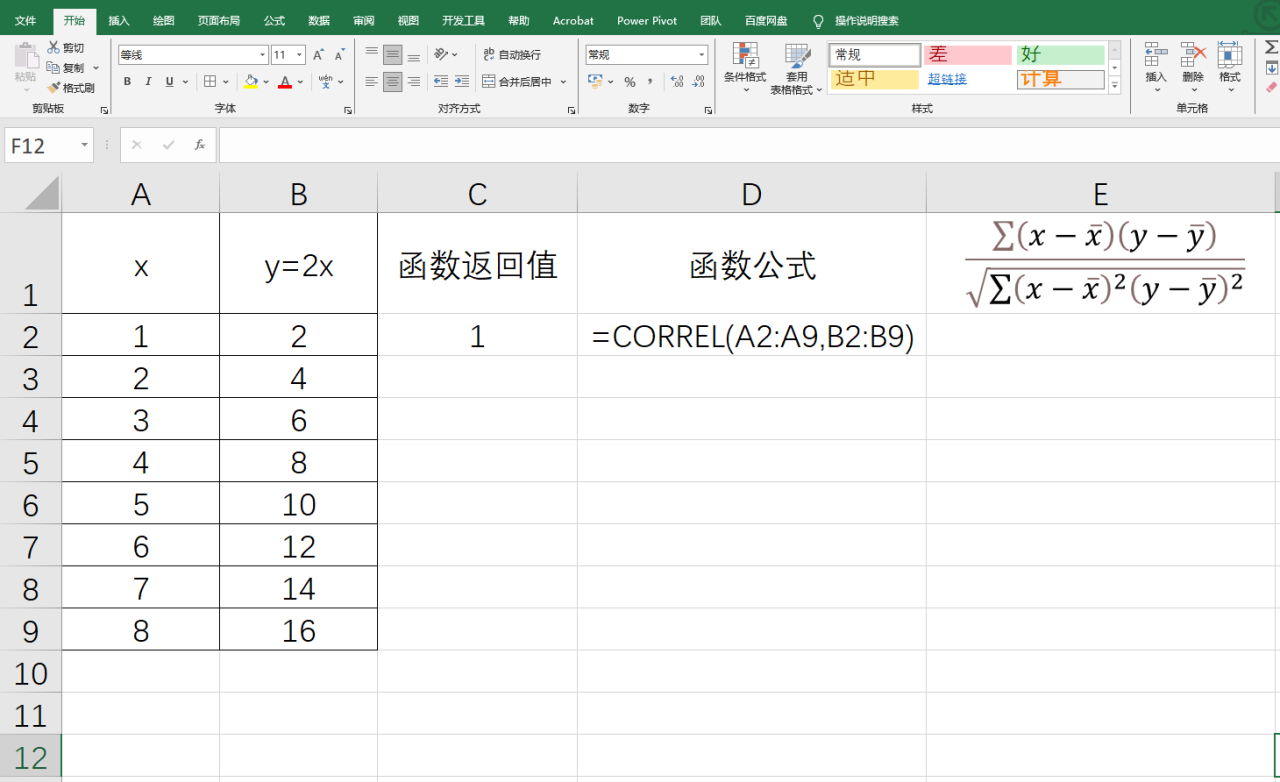
再试试最原始的计算方法返回相关系数

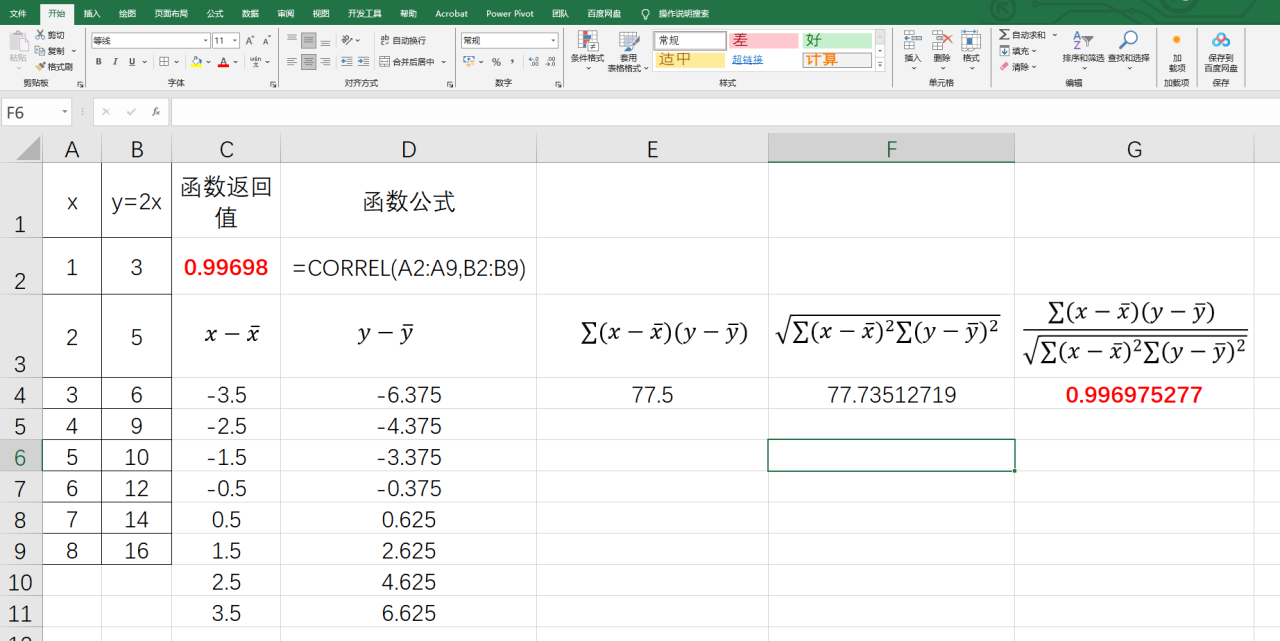
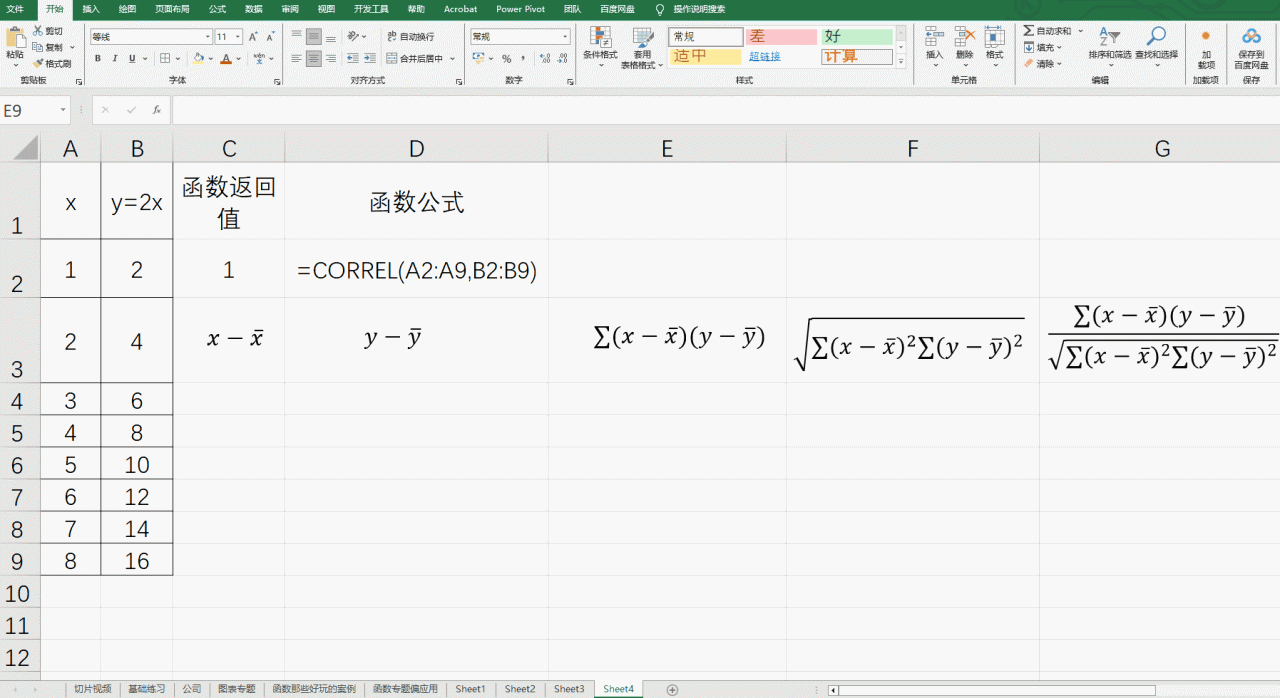
求x- 的函数 =A2-AVERAGE($A$2:$A$9)

求y- 的函数=B2-AVERAGE($B$2:$B$9)

求

的函数=SUMPRODUCT(C4:C11,D4:D11)

求

的函数=SQRT(SUMPRODUCT(C4:C11,C4:C11)*SUMPRODUCT(D4:D11,D4:D11))

从上面的对比我们是明显看出来，通过CORREL公式返回相关系数是最简单的

当然如果需要过程量的话还需用最原始的方式才能把过程量的各个结果都记录下来。

另外还需要对AVERAGE，SUMPRODUCT，SQRT等函数有着比较的熟悉，还需要对于绝对引用相对引用的知识点掌握