KURT返回一组数据的峰值。
峰值的公式为
![]()
上面s为样本的标准差又叫标准偏差
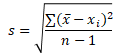
峰值反映与正态分布相比某一分布的相对尖锐度或平坦度。
正峰值表示相对尖锐的分布,可以简单的理解为他的峰值曲线变化比较陡峭
负峰值表示相对平坦的分布,可以简单的理解为他的峰值曲线变化比较平缓
我们先看一下KURT的基本使用
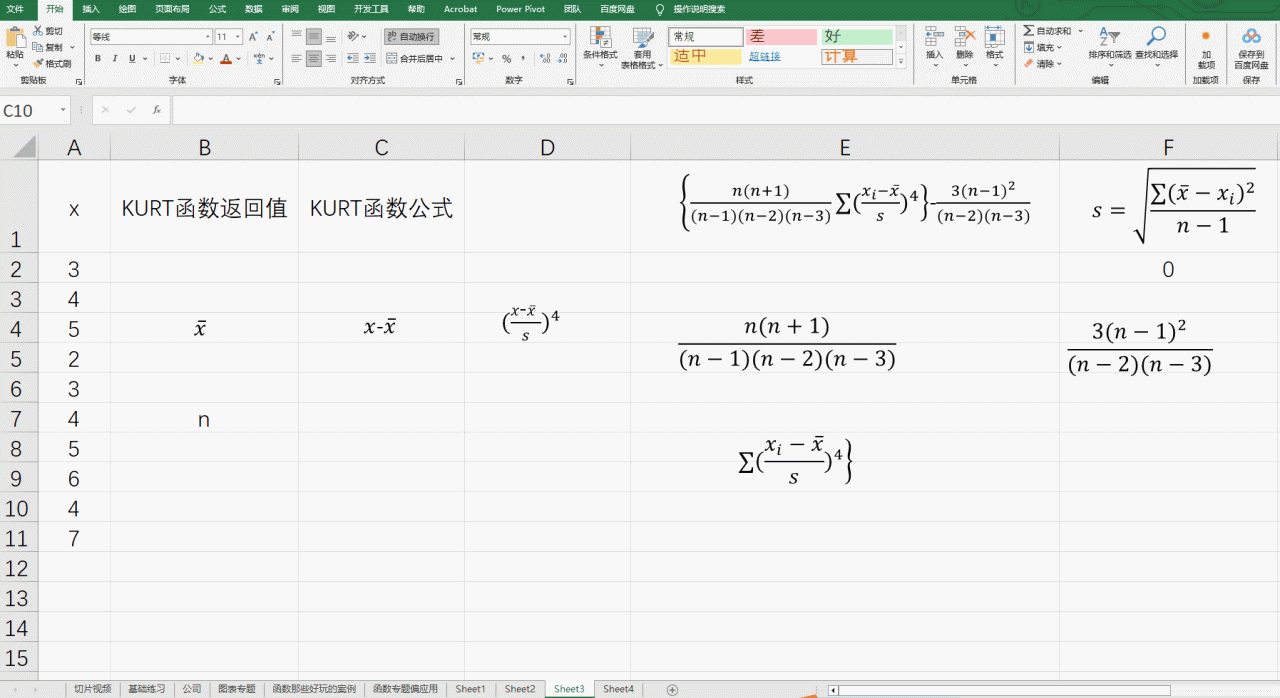
| x | KURT函数返回值 | KURT函数公式 |
| 3 | -0.151799637 | =KURT(A2:A11) |
| 4 | ||
| 5 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 4 | ||
| 7 |
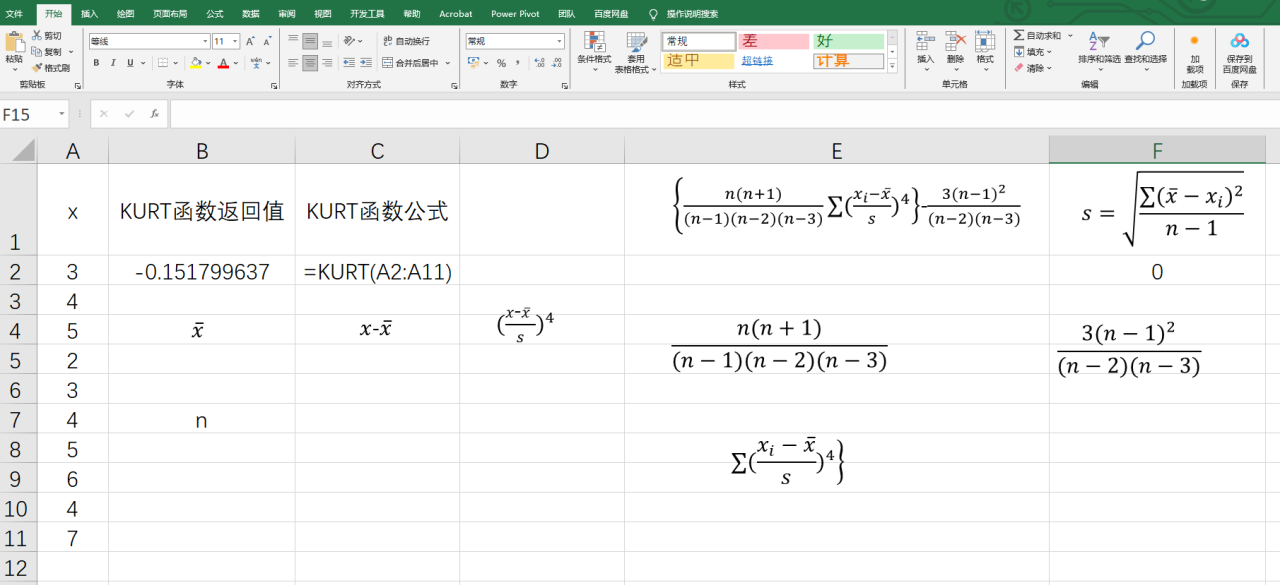
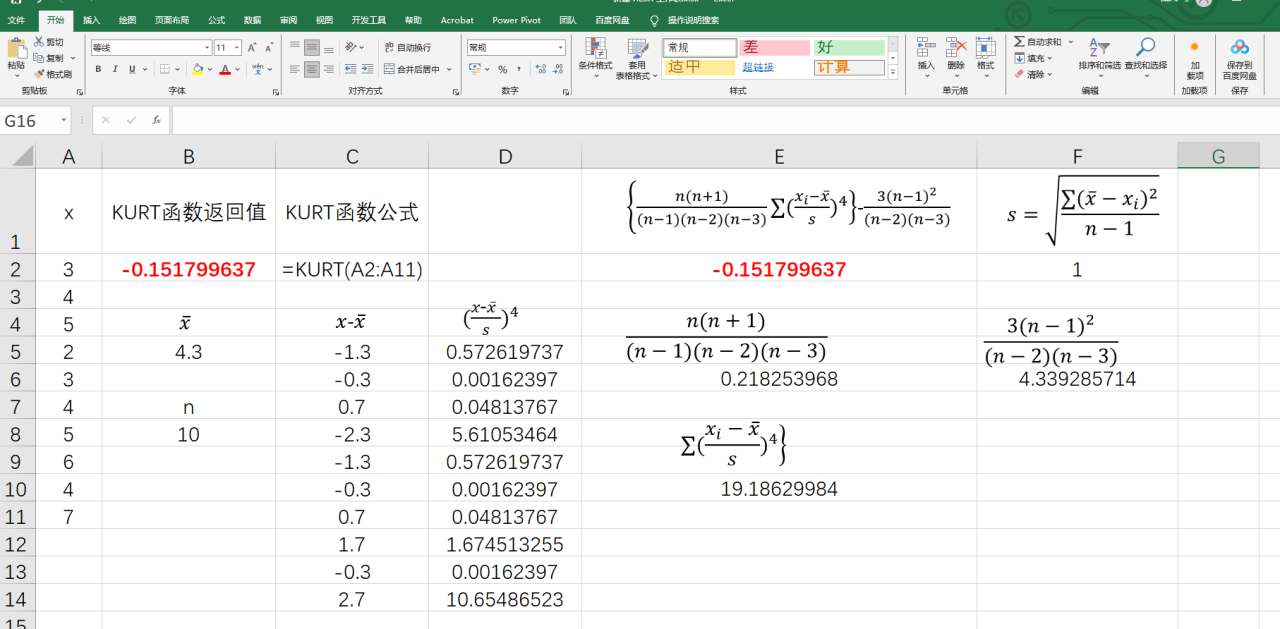
KURT根据公式推导返回值
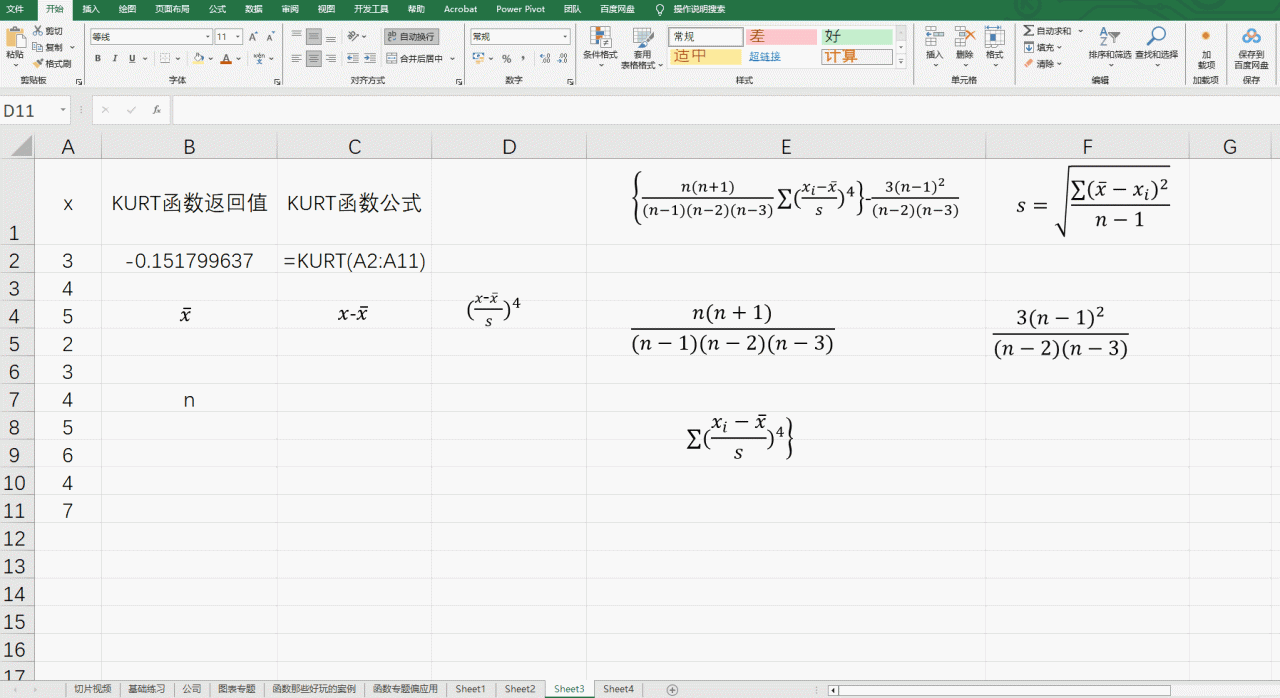
上面的动图有点长
牵扯到的公式如下:另外既然学习函数,函数的基础知识应该是有着一定了解,相对引用和绝对引用的知识是一定要掌握的,如果不太懂,数据的位置一定要跟图中的一样,不同的表同样是A8返回结果是不一样的,懂得话了解基本原理请任意浪。
求样本标准方差s的
=POWER(SUMPRODUCT(C5:C14,C5:C14)/(B8-1),1/2)
求
=(C5/$F$2)^4
求
![]()
=B8*(B8 1)/((B8-1)*(B8-2)*(B8-3))
求
![]()
=3*(B8-1)^2/((B8-2)*(B8-3))
求
![]()
=SUM(D5:D14)










评论 (0)