BASE函数是将十进制的数,转化为其他进制的函数。
在学习这个函数之前你需要对进制有着基本的了解,你才能懂这个函数。
十进制
我们先以10进制为例,再类比其他的进制就容易理解了
比如十进制数56
56有两个位,个位和十位,个位和十位都有它各自的权重
十位的权重是10的1次方
个位的权重是10的0次方
所以56实际上是5*10^1 6*10^1=56
再举例十进制数156,
个位权重是10的0次方也就是10^0=1(也可以认为从右数第1个,是进制(十进制就是10)的0次方)
十位权重是10的1次方也就是10^1=10(也可以认为从右数第2个,是进制(十进制就是10)的1次方)
百位权重是10的2次方也就是10^2=100(也可以认为从右数第3个,是进制(十进制就是10)的2次方)
所以156实际上是1*10^2 5*10^1 6*10^1=156
更多的位数以此类推
其他进制
其他进制我们常用的有二进制,八进制,十六进制
另外你需要了解的是
二进制数任意一个位只能是0和1
八进制数任意一个位只能是0,1,2,3,4,5,6,7
十进制数任意一个位只能是0,1,2,3,4,5,6,7,8,9
十六进制数用ABCDEF分别代表10,11,12,13,14,15,所以十六进制的任意一个位只能是0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
二进制
比如一个二进制数11
我们类比十进制
右边数第一个1的权重的2的0次方也就是2^0=1
右边数第二个1的权重的2的1次方也就是2^1=2
所以二进制的11代表的就是十进制的1*2^1 1*2^0=3
比如一个二进制数111
右边数第一个1的权重的2的0次方也就是2^0=1
右边数第二个1的权重的2的1次方也就是2^1=2
右边数第三个1的权重的2的2次方也就是2^2=4
所以二进制的111代表的就是十进制的1*2^2 1*2^1 1*2^0=7
比如一个二进制数10
右边数第一个1的权重的2的0次方也就是2^0=1
右边数第二个1的权重的2的1次方也就是2^1=2
所以二进制的10代表的就是十进制的1*2^1 0*2^0=2
十六进制
比如一个十六进制数1F
我们类比十进制
右边数第一个1的权重的16的0次方也就是16^0=1
右边数第二个F的权重的2的1次方也就是16^1=16
所以二进制的1F代表的就是十进制的1*16^1 15*2^0=31(上面说过F代表15)
了解上面的之后我们再看看BASE函数
上面我们随便举了几个例子
比如二进制的11代表十进制的3
二进制的111代表十进制的7
二进制的10代表十进制的2
十六进制的1F代表十进制的31
我们通过BASE函数验证,
将十进制的数2,3,7转化为二进制
将十进制的数31转化为十六进制
BASE参数说明
BASE(Number, Radix [Min_length])
BASE 函数语法具有下列参数。
- Number 必需。 要转换的号码。 必须是大于或等于 0 且小于 2^53 的整数。
- Radix 必需。 要将数字转换为的基本基数。 必须是大于或等于 2 且小于或等于 36 的整数。
- Min_length 可选。 返回的字符串的最小长度。 必须是大于或等于 0 的整数。
使用的时候要注意BASE函数的限制
BASE(十进制的整数, 要转化为几进制的数)
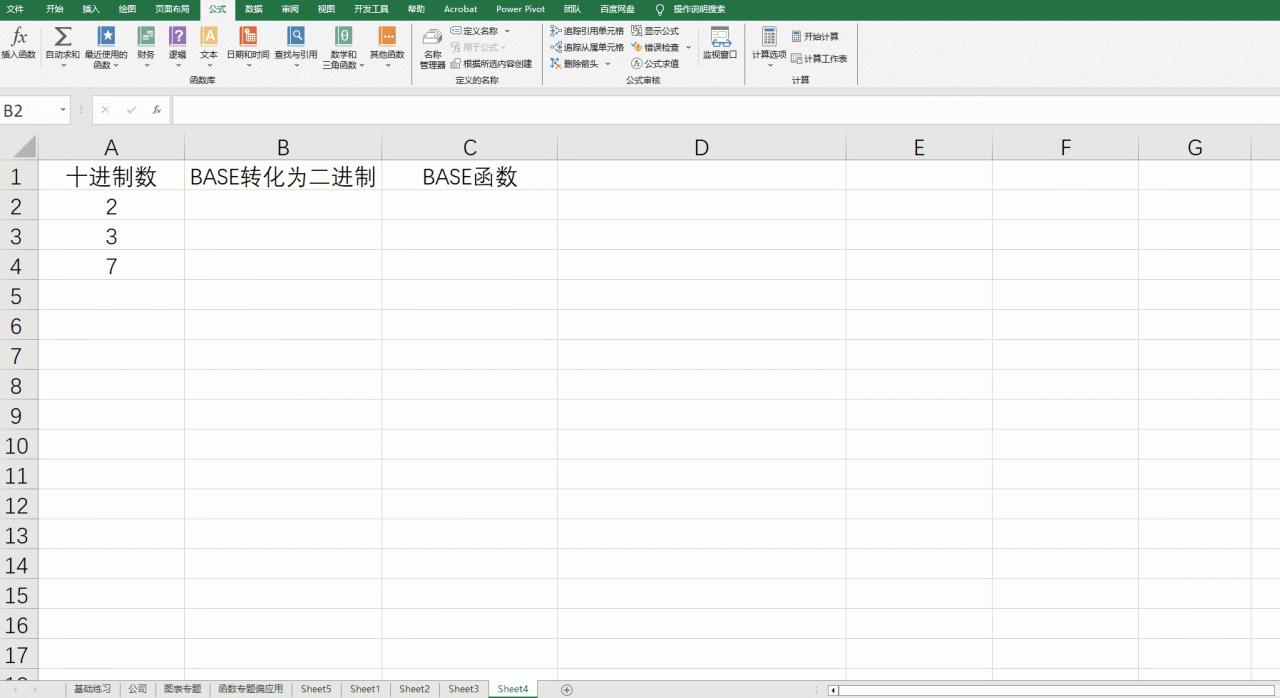
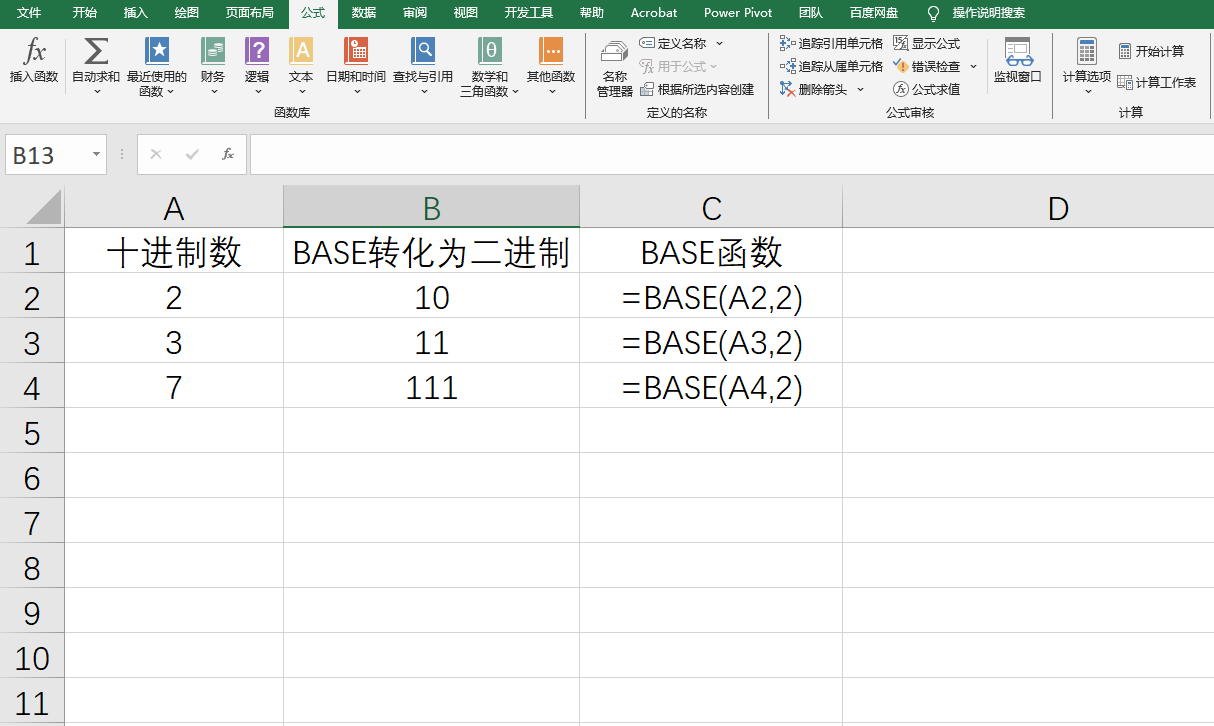

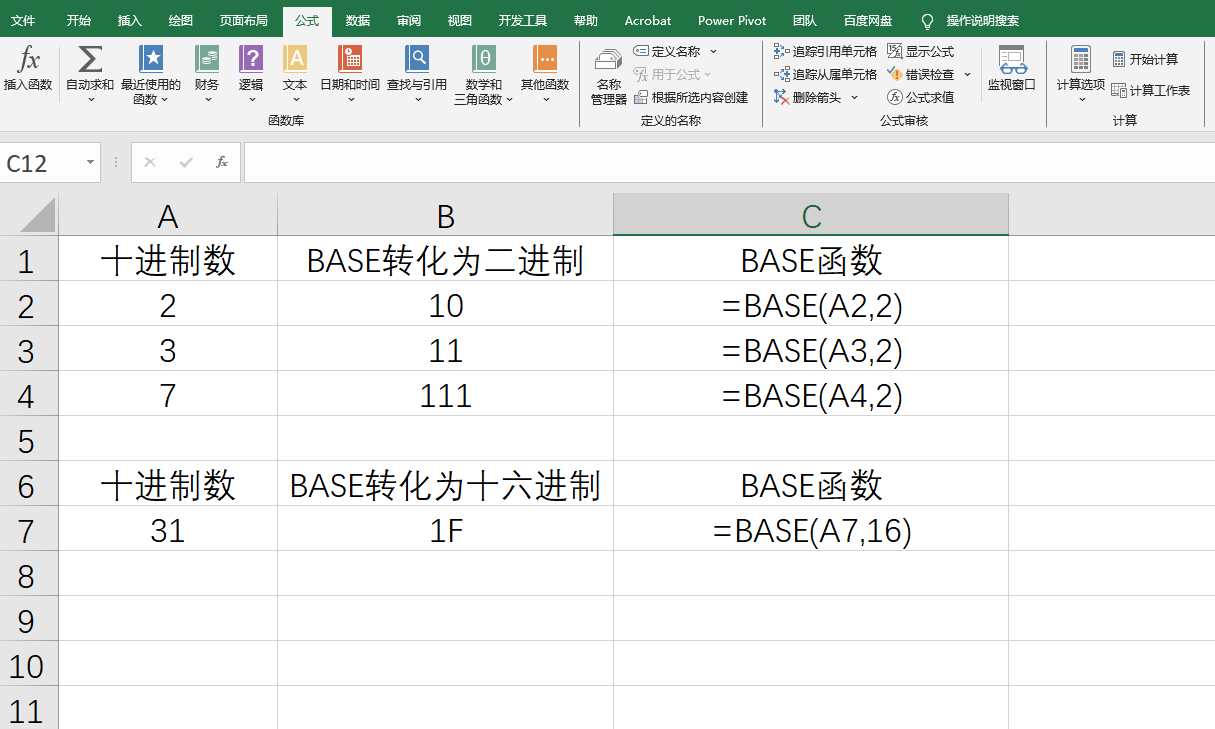
下面是官方关于BASE函数的说明,内容很少,使用也很简单,但是要理解这个函数,还需要上面的很多铺垫





评论 (0)